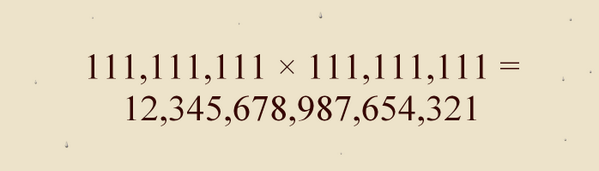In feite is hier uitgerekend (108+ 107
+ 106 + 105 + 104 + 103 + 102
+ 101 + 100)2
Bekend is het kwadrateren van bijvoorbeeld (a + b + c + d).
Dat levert kwadraten en dubbele producten op:
(a + b + c + d)2 = a2 + b2
+ c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd + 2cd
De uitkomst van 111111111 2 is een getal met 17 posities (iets groter dan
1016, een 1 met 16 nullen)
Op de eerste positie komt een 1, namelijk de coëfficiënt van
(108)2 = 1016
Op de tweede positie komt de coëfficiënt van 1015.
Die komt van de term met het dubbele product 108
x 107 dus dat wordt 2.
(met tweetallen uit de reeks 8, 7, 6, 5, 4, 3, 2, 1, 0 kun
je alleen 15 vormen met 8 + 7)
Op de derde positie komt de coëfficiënt van 1014.
Die komt van de termen: het kwadraat van 107 en
het dubbele product 108 x 106 dus dat wordt 3
Op de vierde positie komt de coëfficiënt van 1013.
Die komt van de dubbele producten 108 x 105
en 107 x 106 en dat wordt dus 4
De coëfficiënt van 1012 is 1 + 2 + 2 = 5, want 12 kun je schrijven als 6 + 6 (kwadraat),
8 + 4 en 7 + 5 (dubbele producten)
De coëfficiënt van 1011 is 2 + 2 + 2 = 6, want 11
kun je schrijven als 8 + 3, 7 + 4 en 6 + 5
De coëfficiënt van 1010 is 1 + 2 + 2 + 2 = 7,
want 10 kun je schrijven als 5 + 5, 8 + 2, 7 + 3 en 6 + 4
Merk op dat in de dubbelproducten de termen 101
en 100 tot hier niet aan de orde komen. Die komen eerst nu te pas:
De coëfficiënt van 109 is 2 + 2 + 2 + 2 = 8, want 9 kun je schrijven
als 8 + 1, 7 + 2, 6 + 3 en 5 + 4.
De coëfficiënt van de “middelste” term met macht 108
is 1 + 2 + 2 + 2 = 9, want 8 kun je schrijven als 4 + 4, 8 + 0, 7 + 1, 6 + 2 en
5 + 3.
Na 108 worden de coëfficiënten weer kleiner omdat
het getal van de steeds lagere exponent alleen kan worden gevormd door steeds lagere
getallen uit de reeks 8, 7, 6, 5, 4, 3, 2, 1, 0.
De coëfficiënt van 107 is 2 + 2 + 2 + 2 = 8 want
7 kun je schrijven als 7 + 0, 6 + 1, 5 +
2 en 4 + 3
Je kunt ook achteraan beginnen:
Op de laatste positie komt een 1, namelijk de coëfficiënt
van (100)2 = 1
Op de op één na laatste positie komt de coëfficiënt van 101
= 10
Die komt van term met het dubbele producten 100 x
101 dus dat wordt 2.
Op de volgende positie komt de coëfficiënt van 102.
Die komt van de termen: het kwadraat van 101 en
he dubbele product 100 x 101
In het algemeen:
(10n
+ 10n-1 + 10n-2 + … + 102 + 101 +
100)2
102n heeft coëfficiënt 1
102n-1 heeft
coëfficiënt 2 10n x 10n-1 + 10n-1 x 10n
102n-2 heeft
coëfficiënt 3 10n-1
x 10n-1 + 10n
x 10n-2 + 10n-2 x 10n
enzovoort
Voor de “middelste” coëfficiënt moeten we onderscheid maken
tussen een even en oneven aantal enen.
Oneven aantal enen.
We gaan uit van 2n + 1 enen.
(102n + 102n-1 + 102n-2+ …
+ 102 + 101 + 100)2
De “middelste” term bevat de macht 102n
Die wordt gevormd door het kwadraat van 10n
en de dubbele producten met machten met exponenten 2n + 0, 2n-1 + 1, 2n-2 + 2, 2n-3
+ 3 t/m
n+1 + n-1 dus n dubbele producten.
Dat zijn welgeteld 1 + 2n termen.
Dus bij een oneven aantal enen staat in het middel van het
kwadraat het getal 2n + 1.
Dit geldt alleen voor n = 0, 1, 2, 3, 4
Even aantal enen.
Bij (102n+1 + 102n + 102n-1+
… + 102 + 101 + 100)2 is het aantal
enen even.
De “middelste” heeft ook hier de macht met exponent 2n+1.
Die wordt gevormd door de dubbele producten met machten met exponenten
2n + 0, 2n-1 + 1,
2n-2 + 2, 2n-3 + 3 t/m n+1
+ n-1. Dat zijn n dubbele producten, dus 2n termen.
Dus de “middelste” tem heeft coëfficiënt 2n.
Dit geldt alleen voor n = 1, 2, 3, 4
Want met 10 enen krijg je (helaas):
1111111111 x 1111111111 = 1234567900987654321
Van rechts af bekeken: de 0 van de 10 staat
er wel, maar de 1 van de 10 komt bij de 9 links ervan opgeteld, dus die veranderd weer in 10, waarvan je weer alleen de 0 ziet, terwijl de 1 weer opgeteld wordt bij de
linkerbuur 8 en dus 9 wordt. Daarna loopt het weer zoals het zou moeten.